Calculate the Standard Deviation of a Portfolio
Standard deviation is a term used in probability theory and statistics to measure the variability of a set of data. A low standard deviation means that the data points tend to assemble close to the mean while a high standard deviation indicates that the data tends to spread out over a larger range. In finance, the standard deviation can help analyze annual investment returns to measure volatility associated with an investment or across a portfolio.
Standard Deviation v. Expected Return
While the standard deviation is calculated to help an investor measure investment or portfolio volatility, expected return is computed by inputting the weighted average of the expected returns of each individual investment within the portfolio. In other words, the expected return represents the average of the probability distribution.
Click here to launch the Stock Research Pro Expected Return Calculator
To Use the Stock Research Pro Portfolio
Standard Deviation Calculator
(1) Enter the Investment Year in the Year column
(2) Enter the annual returns associated with each investment
(3) Enter the percentage that each investment makes up of the overall portfolio (in the lower box)
The standard deviation of the portfolio calculates automatically.

________________________________________________________________
The above information is educational and should not be interpreted as financial advice. For advice that is specific to your circumstances, you should consult a financial or tax advisor.
 |
| 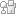 |
|  |
|  |
|  |
|  |
| 
« Minimize Portfolio Risk Through Asset Class Selection | Home | Calculate the Sharpe Ratio »

Recent Posts
- How to Calculate a Stock Market Profit
- Three Basic Financial Concepts for Investors
- Understand an Calculate the Capital Asset Pricing Model (CAPM)
- Calculate Your Retirement Savings Requirements
- The Basics of Stock Market Futures Trading
- How to Calculate Internal Rate of Return (IRR)
- How to Calculate Earnings per Share
- What the Par Value of a Stock Means
- Bond Value Calculator
- Some Basic Forex Trading Tips
Categories
Additional resources
- 홀덤사이트
- Non Gamstop Casino
- Casinos Not On Gamstop
- Migliori Casino Non Aams
- Migliori Casino Online 2025
- Meilleur Casino En Ligne
- Casinos Not On Gamstop
- Non Gamstop Casino
- Casino Sites Not On Gamstop
- Siti Casino Non Aams
- Non Gamstop Casino
- Non Gamstop Casino Sites UK
- UK Casino Not On Gamstop
- Meilleur Casino En Ligne
- UK Online Casinos Not On Gamstop
- I Migliori Casino Non Aams
- New Casino Sites UK
- Best Non Gamstop Casinos
- Casino Not On Gamstop
- Non Gamstop Casinos UK
- Online Betting Sites UK
- Casinos Not On Gamstop
- Casino Not On Gamstop
- Casinos Not On Gamstop
- Best Betting Sites Not On Gamstop
- Slots Not On Gamstop
- Casino En Ligne Crypto
- Casino Online Migliori
- Sites De Paris Sportifs Autorisés En Belgique
- Casino En Ligne Belgique
- Casinos En Ligne France
- KYC 인증 없는 카지노
- Nouveau Casino En Ligne Fiable
- I Migliori Siti Poker Online Aams
- Casino Senza KYC
- Casino Senza Verifica Documenti
- 무료슬롯 사이트
- Meilleur Casino En Ligne France
- Casino En Crypto




Comments
Good work, very simple & easy to use.
May I suggest that you expand the number of years to 10 and the number of investments to 12.
Sincerely,
Basil Apostolou
Toledo, OH USA
Leave a Comment
You must be logged in to post a comment.